【超基本】初心者に贈るアルゴリズム論 ~ダイクストラ法~
スポンサーリンク
最短経路問題
最短経路問題とは,重み付きグラフが与えられたとき,2つの頂点間の重みが最小(距離が最短)となるような経路を求める問題です.
最短経路問題は3つに分けられます.
2頂点対最短経路問題
2つの頂点が与えられ,それらの最短経路を求める問題
単一始点最短経路問題
1つの頂点が与えられ,その頂点からその他のすべての頂点までの最短経路を求める問題
全頂点対最短経路問題
グラフ内のすべての2頂点の組み合わせについての最短経路を求める問題
ダイクストラ法
ダイクストラ法は単一始点最短経路問題で使われる方法です.
すべての経路を計算するより計算量を減らすことができます.
アルゴリズムは以下のようになっています.
集合Xに属する頂点だけを通る経路だけに限定して始点sからの最短経路を求める手続きである.集合Xを始点sだけを含む初期状態から全頂点集合になるまで順次拡大していけば,最終的に正しい最短経路が求まる.具体的には,D[u]によって始点sから頂点uまでの最短経路の長さ,つまり頂点uの距離を表すことにする.集合Xの頂点uについては距離D[u]が正しく求められていれば,集合Xの外にあってXの頂点uと辺で結ばれている頂点vに対して,uを経由してvに至る最短経路の長さをD[u]+c(u,v)として求めることができる.この長さが頂点vに対して以前に求まっている最短経路の長さよりも短いなら,D[u]=D[u]+c(u,v)(ママ)として新たな経路の長さを記録しておく.Xの外の頂点でD[.]の値が最小である頂点をuとすると,uまでの最短経路は上記の操作で求められていることがわかる.したがって,uをXに加えて次のステップに進むことができる.
※ D[u]=D[u]+c(u,v)は間違いで正しくはD[v]=D[u]+c(u,v)です.
例えば,以下のようなグラフの最短経路を求めるとします.(グラフはページ下部の参考文献を参考に作成)

始点s以外へのコストは∞で初期化します.
そうしたら,初めにsをXに入れてあげましょう.

次に,Xの要素はsだけなので,sから到達できる頂点までのコストを更新します.
あとはひたすらこの作業を繰り返します.

sから一番近い頂点dをXに入れます

Xの要素にdが加わったので,dから到達できる頂点までのコストを更新します.
しかし,dから到達できる頂点はeのみで,sから向かった方が近いので変更はなしです.
sから二番目に近いaをXに入れます.(eも距離は同じですが,ここではアルファベット順とします.)

aから到達できる頂点までのコストを更新します.

以下,こんな感じです.
eを追加

c,f更新
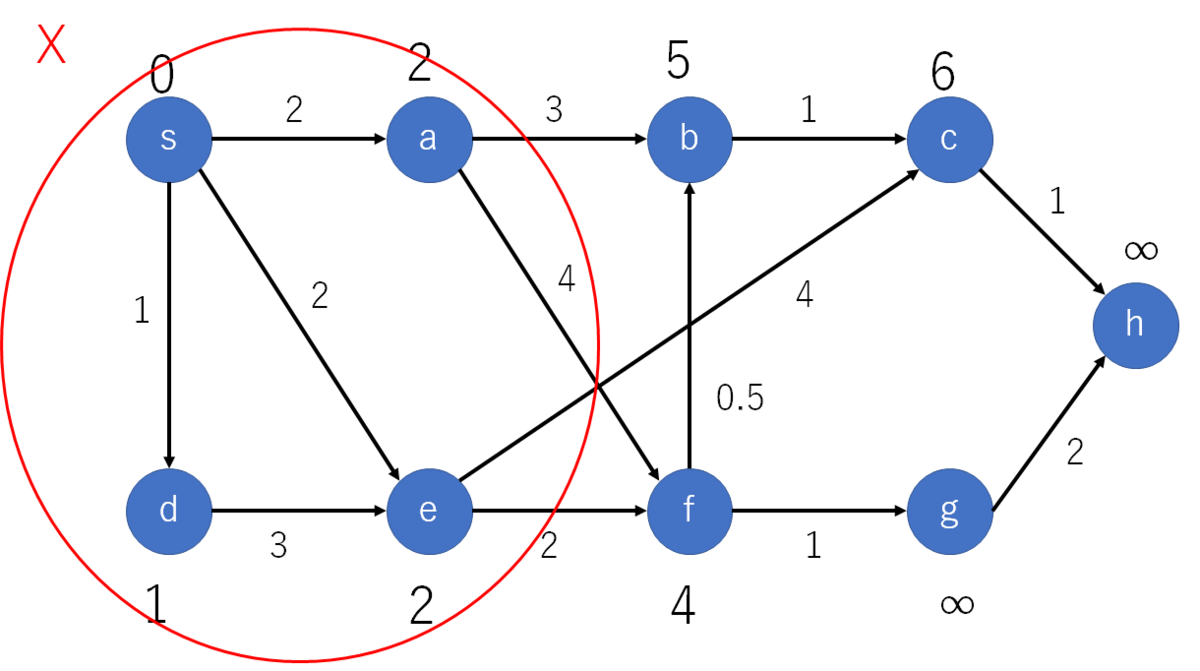
fを追加

b,g更新

bを追加

cを更新

gを追加

hを更新

cを追加

hを更新

hを追加

実装例
上で挙げた図の最短経路を求めるプログラムです.
M = 1000 # 無限 node = 'sabcdefgh' # 出力用 # 重み付き有向グラフ g = [[M, 2, M, M, 1, 2, M, M, M], # s [M, M, 3, M, M, M, 4, M, M], # a [M, M, M, 1, M, M, M, M, M], # b [M, M, M, M, M, M, M, M, 1], # c [M, M, M, M, M, 3, M, M, M], # d [M, M, M, 4, M, M, 2, M, M], # e [M, M, 0.5, M, M, M, M, 1, M], # f [M, M, M, M, M, M, M, M, 2], # g [M, M, M, M, M, M, M, M, M]] # h def dijkstra(s): # 初期化 cost = [M] * len(g) # 重み visit = [0] * len(g) # 訪問済み or 未訪問 parent = [-1] * len(g) # 親ノード # 始点へのコストは0 cost[s] = 0 for i in range(len(g)): mini = M # 最小コスト for j in range(len(g[s])): # 一番近いノードを探す if visit[j] == 0 and cost[j] < mini: mini = cost[j] u = j visit[u] = 1 print('add:' + node[u]) for j in range(len(g[s])): # 他のノードを経由して距離が短くなるなら経路を更新 if cost[u] + g[u][j] < cost[j]: cost[j] = cost[u] + g[u][j] parent[j] = u print(cost) print('\n--result--') for i in range(1, len(g)): print('cost from ' + node[s] + ' to ' + node[i] +' is ' + str(cost[i])) print(node[i] + '\'s parent is ' + node[parent[i]] + '\n') dijkstra(0)
add:s [0, 2, 1000, 1000, 1, 2, 1000, 1000, 1000] add:d [0, 2, 1000, 1000, 1, 2, 1000, 1000, 1000] add:a [0, 2, 5, 1000, 1, 2, 6, 1000, 1000] add:e [0, 2, 5, 6, 1, 2, 4, 1000, 1000] add:f [0, 2, 4.5, 6, 1, 2, 4, 5, 1000] add:b [0, 2, 4.5, 5.5, 1, 2, 4, 5, 1000] add:g [0, 2, 4.5, 5.5, 1, 2, 4, 5, 7] add:c [0, 2, 4.5, 5.5, 1, 2, 4, 5, 6.5] add:h [0, 2, 4.5, 5.5, 1, 2, 4, 5, 6.5] --result-- cost from s to a is 2 a's parent is s cost from s to b is 4.5 b's parent is f cost from s to c is 5.5 c's parent is b cost from s to d is 1 d's parent is s cost from s to e is 2 e's parent is s cost from s to f is 4 f's parent is e cost from s to g is 5 g's parent is f cost from s to h is 6.5 h's parent is c
