Java Gold合格への道 ~JDBC・ResultSetにおけるレコード挿入~
こんにちは。たろすです。
今回はJDBCのResultSetにおけるレコード挿入について説明します。
使い方
以下のようなテーブルを使用します。

public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身で設定したユーザ名 final String PASS = "****"; // 自身で設定したパスワード try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_UPDATABLE); ResultSet rs = st.executeQuery("SELECT * FROM employee")) { rs.moveToInsertRow(); rs.updateString(1, "000007"); rs.updateString(2, "柴田 敏夫"); rs.updateDate(3, Date.valueOf("2022-06-01")); rs.updateDate(4, Date.valueOf("1990-03-08")); rs.insertRow(); System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); } catch (SQLException e) { e.printStackTrace(); } } }
000007 柴田 敏夫 2022-06-01 1990-03-08
createStatementメソッドの第二引数はResultSet.CONCUR_UPDATABLEにします。
Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_UPDATABLE);
ResultSetにはレコード挿入用の行があります。
その位置にカーソルを動かします。
rs.moveToInsertRow();
その後はUPDATEの時と同じようにupdate~メソッドでカラム(第一引数)と値(第二引数)を指定し、insertRowメソッドで挿入します。
rs.updateString(1, "000007"); rs.updateString(2, "柴田 敏夫"); rs.updateDate(3, Date.valueOf("2022-06-01")); rs.updateDate(4, Date.valueOf("1990-03-08")); rs.insertRow();
実行後のデータベーステーブルは以下のようになります。

Java Gold合格への道 ~JDBC・更新可能なResultSet~
こんにちは。たろすです。
今回はJDBCにおける更新可能なResultSetについて説明します。
使い方
以下のようなテーブルを使用します。

public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身で設定したユーザ名 final String PASS = "****"; // 自身で設定したパスワード try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_UPDATABLE); ResultSet rs = st.executeQuery("SELECT * FROM employee")) { rs.absolute(4); rs.updateString(2, "源田 一郎"); rs.updateRow(); System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); } catch (SQLException e) { e.printStackTrace(); } } }
000004 源田 一郎 2022-05-01 1995-01-08
更新可能なResultSetを使用する場合、createStatementメソッドの第二引数をResultSet.CONCUR_UPDATABLEにする必要があります。
Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_UPDATABLE);
続いて、更新したいレコードにカーソルを合わせ、update~メソッドで更新するカラム(第一引数)と値(第二引数)を指定します。
最後にupdateRowメソッドを呼ぶことで更新内容をデータベースに反映させます。
rs.absolute(4); rs.updateString(2, "源田 一郎"); rs.updateRow();
コード実行後のデータベーステーブルは以下のようになっており、反映されていることがわかります。

Java Gold合格への道 ~JDBC・スクロール~
こんにちは。たろすです。
今回はJDBCにおけるスクロールについて説明します。
使い方
以下のテーブルを使用します。

public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身で設定したユーザ名 final String PASS = "****"; // 自身で設定したパスワード try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_READ_ONLY); ResultSet rs = st.executeQuery("SELECT * FROM employee")) { rs.last(); // 最終行に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.first(); // 先頭行に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.afterLast(); // 最終行の次に移動 rs.previous(); // 1つ前に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.beforeFirst(); // 先頭行の前に移動 rs.next(); // 1つ次に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.relative(3); // 3つ順方向に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.relative(-2); // 2つ逆方向に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); rs.absolute(5); // 5番目の行に移動 System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); } catch (SQLException e) { e.printStackTrace(); } } }
000006 市川 誠 2022-05-03 1996-12-10 000001 伊藤 太郎 2022-04-01 1985-11-02 000006 市川 誠 2022-05-03 1996-12-10 000001 伊藤 太郎 2022-04-01 1985-11-02 000004 源田 三郎 2022-05-01 1995-01-08 000002 坂本 啓介 2022-04-01 1972-05-21 000005 斉藤 正治 2022-05-01 1991-09-01
スクロールできるようにするにはcreateStatementメソッドの第一引数でResultSet.TYPE_SCROLL_INSENSITIVEかResultSet.TYPE_SCROLL_SENSITIVEを設定する必要があります。
Statement st = con.createStatement(ResultSet.TYPE_SCROLL_INSENSITIVE, ResultSet.CONCUR_READ_ONLY);
INSENSITIVEはResultSetのもとになっているデータに対する変更を反映しない、SENSITIVEは反映するという違いがあります。
また、第二引数はResultSetによるレコードの更新可否の有無を指定します。
更新不可にするときはResultSet.CONCUR_READ_ONLY、更新可能にするときはResultSet.CONCUR_UPDATABLEを指定します。
rs.last(); // 最終行に移動
lastメソッドはカーソルを最終行に移動します。
そのため6番目のレコードが表示されます。
rs.first(); // 先頭行に移動
firstメソッドはカーソルを先頭行に移動します。
そのため1番目のレコードが表示されます。
rs.afterLast(); // 最終行の次に移動 rs.previous(); // 1つ前に移動
afterLastメソッドはカーソルを最終行の次に移動します。
また、previousメソッドはカーソルを1つ前に移動します。
そのため最終行のレコードが表示されます。
rs.beforeFirst(); // 先頭行の前に移動 rs.next(); // 1つ次に移動
beforeFirstはカーソルを先頭行の前に移動します。
また、nextメソッドはカーソルを1つ次に移動します。
そのため先頭行のレコードが表示されます。
rs.relative(3); // 3つ順方向に移動
relativeメソッドは引数の数だけカーソルを順方向に移動します。
relativeメソッドを実行する前のカーソルは先頭行を指していたため、4番目のレコードが表示されます。
rs.relative(-2); // 2つ逆方向に移動
relativeメソッドの引数に負の値を入れるとカーソルは逆方向に移動します。
カーソルは4番目を指していたため、2番目のレコードが表示されます。
rs.absolute(5); // 5番目の行に移動
absoluteメソッドは引数に指定された行番号にカーソルを移動させます。
そのため5番目のレコードが表示されます。
Java Gold合格への道 ~JDBC・基本的な使い方~
こんにちは。たろすです。
今回はJDBCの基本的な使い方について説明します。
検索
以下のようなテーブルを取得します。
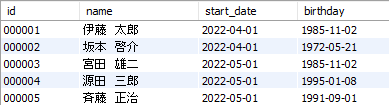
public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身が設定したユーザ名 final String PASS = "****"; // 自身が設定したパスワード try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement(); ResultSet rs = st.executeQuery("SELECT * FROM employee")) { while (rs.next()) { System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); } } catch (SQLException e) { e.printStackTrace(); } } }
000001 伊藤 太郎 2022-04-01 1985-11-02 000002 坂本 啓介 2022-04-01 1972-05-21 000003 宮田 雄二 2022-05-01 1985-11-02 000004 源田 三郎 2022-05-01 1995-01-08 000005 斉藤 正治 2022-05-01 1991-09-01
順番に見ていきましょう。
final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身が設定したユーザ名 final String PASS = "****"; // 自身が設定したパスワード
URLは次のような形式をしています。
jdbc:データベース製品名://ホスト名[:ポート番号]/データベース名[?オプション]
今回のデータは日本語を含むため、オプションで文字コードを指定しています。
try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement(); ResultSet rs = st.executeQuery("SELECT * FROM employee")) {
上から順番にデータベースへの接続、Statementオブジェクトの生成、クエリの実行を行っています。
executeQueryメソッドの戻り値はResultSetオブジェクトになっています。
それぞれ使用後はクローズする必要があるため、try-with-resourcesを使用しています。
while (rs.next()) { System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); }
ResultSetのカーソルは、最初は一つ目のレコードの上を指しています。
nextメソッドを呼ぶことで一つ目のレコードを指し、その後も二つ目、三つ目のレコードと順番に降りていきます。
getStringメソッドはString型で引数の列の値を取得します。
getDateメソッドも同様にDate型で取得します。
get~メソッドは引数に列名をとるオーバーロード・メソッドもあります。
更新
先ほどのテーブルに6番目のレコードを追加します。
public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身が設定したユーザ名 final String PASS = "****"; // 自身が設定したパスワード int result = -1; try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement()) { result = st.executeUpdate("INSERT INTO employee" + "(id, name, start_date, birthday) " + "VALUES ('000006', '市川 誠', '20220503', '19971210')"); } catch (SQLException e) { e.printStackTrace(); } if (result > 0) { System.out.println("更新成功"); } else { System.out.println("更新失敗"); } } }
更新成功
result = st.executeUpdate("INSERT INTO employee" + "(id, name, start_date, birthday) " + "VALUES ('000006', '市川 誠', '20220503', '19971210')");
SELECTではexecuteQueryメソッドを使ったのに対し、UPDATEやINSERT、DELETE、DDLのSQLを発行する際はexecuteUpdateメソッドを使用します。
if (result > 0) { System.out.println("更新成功"); } else { System.out.println("更新失敗"); }
exexuteUpdateメソッドの戻り値は更新されたレコード数になっています。
このコードを実行すると以下のように更新されます。

動的な実行
例えば以下のようにSELECTか更新系かどちらが実行されるかわからない場合、executeメソッドを使用します。
public class Main { public static void main(String[] args) { final String URL = "jdbc:mysql://localhost:3306/javagold?characterEncoding=UTF-8"; final String USER = "****"; // 自身が設定したユーザ名 final String PASS = "****"; // 自身が設定したパスワード String[] sql = { "SELECT * FROM employee", "UPDATE employee SET birthday = '1996-12-10' WHERE id = '000006'" }; int index = new Random().nextInt(2); try (Connection con = DriverManager.getConnection(URL, USER, PASS); Statement st = con.createStatement()) { boolean isQuery = st.execute(sql[index]); if (isQuery) { ResultSet rs = st.getResultSet(); while (rs.next()) { System.out.print(rs.getString(1) + " "); System.out.print(rs.getString(2) + " "); System.out.print(rs.getDate(3) + " "); System.out.println(rs.getDate(4) + " "); } } else { int updateCount = st.getUpdateCount(); if (updateCount > 0) { System.out.println("更新成功"); } else { System.out.println("更新失敗"); } } } catch (SQLException e) { e.printStackTrace(); } } }
executeメソッドの戻り値はSELECTの場合true、それ以外の場合はfalseになります。
SELECTの場合はgetResultSetメソッドを使用してResultSetを取得できます。
一方でそれ以外の場合はgetUpdateCountメソッドで更新件数を取得できます。
Java Gold合格への道 ~並行処理・Fork/Joinフレームワーク~
こんにちは。たろすです。
今回は並行処理におけるFork/Joinフレームワークについて説明します。
Fork/Joinフレームワークとは
Forkは分割、Joinは結合を意味しています。
つまり、Fork/Joinフレームワークはタスクを分割して実行し、結果を結合するフレームワークです。
以下のように使用します。
public class Task extends RecursiveTask<String> { @Override protected String compute() { return "Task ended"; } }
public class Main { public static void main(String[] args) { try { ForkJoinPool executor = new ForkJoinPool(); ForkJoinTask<String> result = executor.submit(new Task()); System.out.println(result.get()); } catch (InterruptedException | ExecutionException e) { e.printStackTrace(); } } }
Task ended
タスクの実装にはRecursiveActionクラスまたはRecursiveTask<V>クラスを継承します。
戻り値がない場合はRecursiveActionクラス、ある場合はRecursiveTask<V>クラスを継承します。
computeメソッドでタスクの処理を実装します。
タスク実行にはexecuteメソッド、invokeメソッド、submitメソッドがあり、以下のように使い分けます。
void execute(ForkJoinTask<?> task):非同期かつ処理結果なし
<T> T invoke(ForkJoinTask<T> task):同期かつ処理結果あり
<T> ForkJoinTask<T> submit(ForkJoinTask<T> task):非同期かつ処理結果あり
上記のコードで使用しているsubmitメソッドは戻り値がForkJoinTaskオブジェクトであり、getメソッドによってcomputeメソッドの戻り値を取り出せます。
Java Gold合格への道 ~並行処理・Callableインタフェース~
こんにちは。たろすです。
今回は並行処理におけるCallableインタフェースについて説明します。
Callableインタフェースとは
マルチスレッドプログラミングで使われるRunnableインタフェースですが、Runnableインタフェースで定義されているrunメソッドは戻り値を返したり、例外をスローしたりできません。
戻り値を返したり、例外をスローしたりしたいときに使用するのがCallableインタフェースです。
Callableインタフェースで定義されているcallメソッドはそれらが可能です。
public class Main { public static void main(String[] args) { Callable<String> task = new Callable<String>() { public String call() throws Exception { return "call"; } }; try { ExecutorService executorService = Executors.newCachedThreadPool(); Future<String> future = executorService.submit(task); System.out.println(future.get()); } catch (Exception e) { e.getStackTrace(); } } }
call
Callableインタフェースを実装するタスクの実行にはExecutorServiceのsubmitメソッドを使用します。
submitの戻り値はFutureオブジェクトで、getメソッドによって中身(callメソッドの戻り値)を取得できます。
Java Gold合格への道 ~並行処理・Executorインタフェース~
こんにちは。たろすです。
今回は並行処理におけるExecutorインタフェースについて説明します。
Executorインタフェースとは
Exexutorインタフェースはタスク送信をタスクの実行方式から分離する方法を提供する、Threadクラスに代わるインタフェースです。
以下のように使用します。
public class Main { public static void main(String[] aargs) { Runnable task = new Runnable() { public void run() { System.out.println("execute"); } }; Executor executor = Executors.newCachedThreadPool(); executor.execute(task); } }
execute
ちなみにこれをThreadクラスを用いて記述すると以下のようになります。
public class Main { public static void main(String[] aargs) { Runnable task = new Runnable() { public void run() { System.out.println("execute"); } }; Thread thread = new Thread(task); thread.start(); } }
なにが違うかというと、Exexutorを使用したタスクの実行ではスレッドの生成とタスクの実行が隠蔽されています。
これによりタスクの実行方式を制御できるようになっています。


