【基本・応用情報技術者】システムの信頼性評価
こんにちは。たろすです。
今回はシステムの信頼性評価について説明します。
信頼性評価指標
システムの信頼性評価の指標としてよく使われるものを二つ挙げます。
稼働率の計算
基本情報技術者試験や応用情報技術者試験では稼働率の計算問題がよく出てきます。
稼働率は以下の式で求められます。
式を言語化すると「全体の時間に占めるMTBF(稼働している時間)の割合」です。
それでは例題を解いてみましょう。
例題
問題
故障してから次に故障するまでの平均時間が990時間の機器がある。故障をすると復旧するまでに平均で10時間かかる。この機器の稼働率を答えよ。
解答
先程挙げた式に当てはめると以下のようになります。
したがって答えは0.99です。
【基本・応用情報技術者】ハミング符号による誤り訂正
こんにちは。たろすです。
今回はハミング符号による誤り訂正について説明します。
ハミング符号とは
ハミング符号とは、データの伝送時に付加し、誤りを検知・訂正できる誤り訂正符号の一つ。
ハミング符号(Hamming code)とは - IT用語辞典 e-Words
とのことです。
誤り制御には検知しかできないものと訂正もできるものがあります。
ハミング符号は1ビットまでの誤りなら訂正もできます。
このような知識もよく問われるので覚えておきましょう。
例題
問題
さっそくですが例題を解いていきます。
応用情報技術者試験からの出題です。
ハミング符号とは,データに冗長ビットを付加して, 1ビットの誤りを訂正できるようにしたものである。ここでは,X1,X2,X3,X4の4ビットから成るデータに,3ビットの冗長ビットP3,P2,P1を付加したハミング符号 X1X2X3P3X4P2P1 を考える。付加ビットP1,P2,P3は,それぞれ
となるように決める。ここで⊕は排他的論理和を表す。
ハミング符号 1110011 には1ビットの誤りが存在する。誤りビットを訂正したハミング符号はどれか。
ア.0110011
イ.1010011
ウ.1100011
エ.1110111
(出典:平成30年度 春期 応用情報技術者試験 午前 問3)
解答
「ハミング符号 X1X2X3P3X4P2P1 を考える」とあり、ハミング符号は「1110011 」であることから、
X1=1
X2=1
X3=1
P3=0
X4=0
P2=1
P1=1
であることがわかります。
それでは3つの式に具体的な数字を入れていきます。
一番目の式は、
となります。
演算結果は1となり0になっていないので、X1かX3かX4が誤っていることがわかります。
二番目の式は
となります。
こちらも演算結果は1となり0になっていないので、X1かX2かX4が誤っていることがわかります。
三番目の式は
となります。
こちらも演算結果は1となり0になっていないので、X1かX2かX3が誤っていることがわかります。
三つの式すべてに誤っているビットが含まれていることがわかりました。
したがって、三つの式すべてに含まれているビットが誤っているビットであると断定できます。
つまり、誤っているビットはX1です。
以上より、答えは「1110011 」から先頭のビットを反転した「ア.0110011 」となります。
【基本・応用情報技術者】オートマトンと状態遷移図
こんにちは。たろすです。
今回はオートマトンと状態遷移図について説明します。
オートマトンとは
オートマトンは一定の規則に従って複数の内部状態の間を遷移する仮想的な機械で、現在の状態と入力の組み合わせを規則の中から探し出し、指定された次の状態へ遷移する。規則に該当する組み合わせがなければ同じ状態を維持する。規則は状態遷移表や状態遷移図として書き表すことができる。
オートマトン(状態機械)とは - IT用語辞典 e-Words
つまり、現在の状態にある入力を与えると特定の状態へ遷移する機械のことです。
オートマトンの問題では状態遷移図がよく使われます。
状態遷移図の読み方
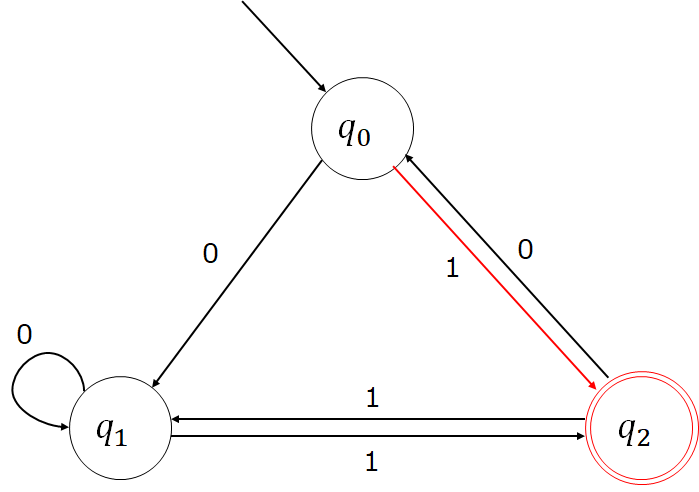
次のような状態遷移図があります。

丸が状態で、矢印が遷移、矢印の横にある値が入力を表しています。
まず最初に確認するのが初期状態と終了状態です。
なにもないところから矢印が入ってきているq0が初期状態、二重丸のq2が終了状態です。

問題としては選択肢としてビット列が与えられて、「次の状態遷移図で表現されるオートマトンで受理されるビット列はどれか」などと問われます。
「受理される」とは入力をすべて入れたときに終了状態になるものを指します。
具体的な読み方は例題を解きながら見ていきましょう。
例題
次の状態遷移図で表現されるオートマトンで受理されるビット列はどれか。

ア.00100
イ.10110
ウ.11110
エ.00111
ア(00100)の解説
初期状態はq0です。

アの最初の入力は0なのでq1に移ります。

次の入力も0なので自己遷移します。

次の入力は1なのでq2に遷移します。

ここで終了状態に到達しましたが、入力がまだあるので続きます。
次の入力は0なのでq0に遷移します。

さらに次の入力も0なのでq1に遷移します。

すべての入力を終えて到達した状態はq1なのでアのビット列は受理されません。
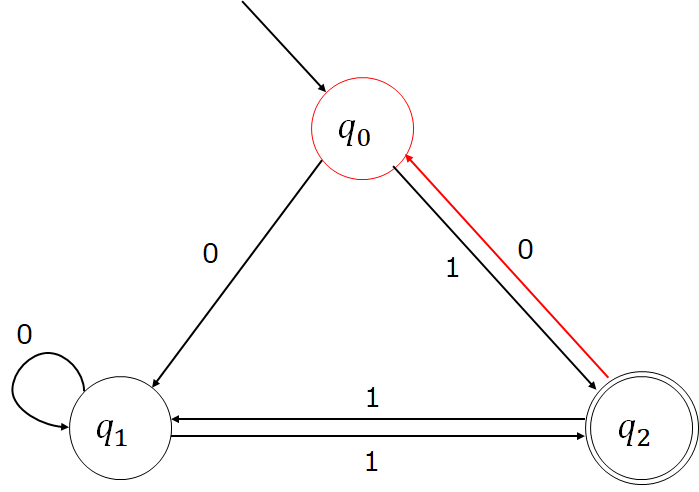
イ(10110)の解説
解き方はアと同様なので詳しい解説は省略します。



ウ(11110)の解説
解き方はアと同様なので詳しい解説は省略します。






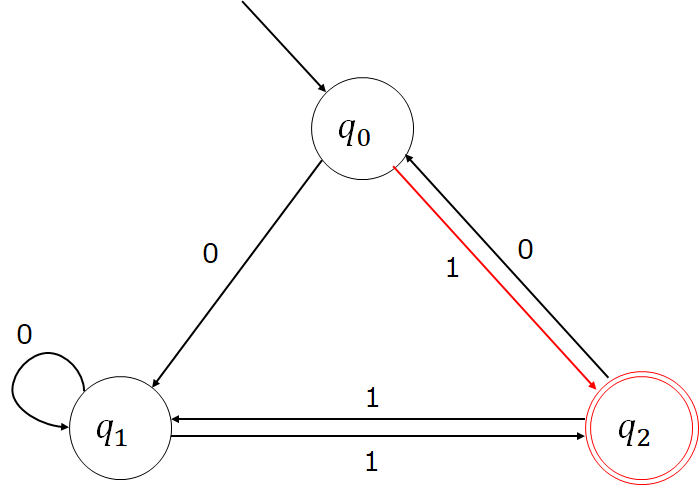
エ(00111)の解説
解き方はアと同様なので詳しい解説は省略します。






最後に到達した状態が終了状態となりました。
したがって答えはエになります。
【基本・応用情報技術者】カルノー図の使い方
こんにちは。たろすです。
今回はカルノー図の使い方を説明します。
カルノーズの使い方
パターン1
例えば以下の論理式を簡略化したいとします。
カルノー図を埋めていきましょう。

まず第1項のを見ます。
AとCは否定になっています。
なので、A=0、B=1、C=0、D=1のところに1を埋めます。

続いて第2項のを見ます。
Aが否定になっています。
そのため、A=0、B=1、C=1、D=1のところに1を埋めます。

1が隣り合っていますね。

このような場合は二つに共通する部分を探しましょう。
するとAが0でBが1、Dが1ということ共通しているとわかると思います。
したがって、最初に与えられた論理式は次のように簡略化できます。
パターン2
次に以下の論理式を簡略化します。
先程と同じようにカルノー図を埋めると次のようになります。

一見すると隣り合っていないように見えますが、実は一番左の列と一番右の列は隣り合っているとみなすことができます。

この二つに共通する部分はAが0でBが1、Dが0ということです。
なので最初に与えられた論理式を簡略化すると、
となります。
なお、一番上の行と一番下の行も隣り合っているとみなします。
パターン3
次の論理式を簡略化します。
カルノー図を書くと、

三つの1が隣り合っています。
しかし、以下のように三つを囲むことはできません。

このような場合は次のように囲みましょう。

赤い方の囲いの共通する部分はAが0でBが1、Dも1ということ、青い方の囲いの共通する部分はAが0でBが1、Cも1ということ。
なので、それらを論理和で繋げて
となります。
このような囲むことができるのは2のべき乗×2のべき乗になる場合だけです。
パターン4
次の論理式を簡略化します。
カルノー図にするとこのようになります。

先程説明した通り、2のべき乗×2のべき乗なら囲えるので、2×2はもちろん囲えます。

これらに共通する部分はBが1でDも1であるということ。
そのため、最初に与えられた論理式を簡略化すると、
となります。
Java Silver合格への道 ~拡張for文の中でArryaList.removeしても例外がスローされない謎に迫る~
こんにちは。たろすです。
Java Silverの勉強をしている中で最も納得いかなかった問題を紹介します。
黒本にはあまり詳しく解説が書かれていなかったのでぜひ見ていただければと思います。
問題
以下のプログラムを実行したときの結果を答えよ。(黒本の問題を改題)
import java.util.ArrayList; public class For1 { public static void main(String[] args) { // TODO 自動生成されたメソッド・スタブ ArrayList<String> array = new ArrayList<>(); array.add("A"); array.add("B"); array.add("C"); array.add("D"); for (String s : array) { if (s.equals("C")) { array.remove(s); } else { System.out.print(s); } } } }
A.「AB」と表示される
B.「ABCD」と表示される
C.「ABD」と表示される
D.例外がスローされる
E.コンパイルエラーが起こる
解答
答えはAです。
私は訳がわかりませんでした。
拡張for文の中でArrayListの要素を操作すると例外がスローされると思っていましたから。
黒本の解説を見ても、
「3番目の要素が削除されたときに4番目の要素が3番目に繰り上がり、次に削除する要素がなくなるため繰返し処理が終了します」
とだけ。
いやいや、そこじゃないんだよ。
なんで例外にならないの?
と非常にもやもやしました。
例外がスローされない理由
実は削除した要素が最後から2番目だから例外がスローされないんです。
ちなみに1番目、2番目、最後の要素を削除すると例外がスローされます。
このときスローされる例外は「ConcurrentModificationException」です。
公式ドキュメントを読んでみる
公式ドキュメントで「ConcurrentModificationException」について調べたところ
この例外は、オブジェクトの並行変更を検出したメソッドによって、そのような変更が許可されていない場合にスローされます。
たとえば、あるスレッドがCollectionで反復処理を行っている間に、別のスレッドがそのCollectionを変更することは一般に許可されません。通常、そのような環境では、反復処理の結果は保証されません。いくつかのイテレータ(Iterator)の実装(JREが提供するすべての一般的な目的のコレクションの実装の、イテレータの実装を含む)は、その動作が検出された場合にこの例外をスローすることを選択できます。この例外をスローするイテレータは、フェイルファストイテレータと呼ばれます。イテレータは、将来の予測できない時点において予測できない動作が発生する危険を回避するために、ただちにかつ手際よく例外をスローします。
とのことです。
どうやら拡張for文の中で要素を削除するとこの例外がスローされるのが正しい挙動のようです。
ArrayListのコードを読んでみる
前提として拡張for文は内部でイテレータを使っています。
ArrayListが継承しているAbstractList
private class Itr implements Iterator<E> { int cursor = 0; int lastRet = -1; int expectedModCount = modCount; public boolean hasNext() { return cursor != size(); } public E next() { checkForComodification(); try { int i = cursor; E next = get(i); lastRet = i; cursor = i + 1; return next; } catch (IndexOutOfBoundsException e) { checkForComodification(); throw new NoSuchElementException(); } } final void checkForComodification() { if (modCount != expectedModCount) throw new ConcurrentModificationException(); } }
拡張for文ではまずhasNextメソッドを実行し、戻り値がtrueならnextメソッドでarray[i]の要素を取り出します。

nextメソッドの頭でcheckForComodificationメソッドを実行しています。
modCountとexpectedModCountが異なるとConcurrentModificationExceptionがスローされます。
次にremoveメソッドのコードを見てみます。
public boolean remove(Object o) { if (o == null) { for (int index = 0; index < size; index++) if (elementData[index] == null) { fastRemove(index); return true; } } else { for (int index = 0; index < size; index++) if (o.equals(elementData[index])) { fastRemove(index); return true; } } return false; }
今回の問題の場合、引数oはnullでないのでelseブロックに入ります。
そしてArryaListのサイズ分インクリメントし、oと等しい要素があればfastRemoveメソッドを実行します。
つまり今回の場合はarray[i]がCのときにfastRemoveが実行されます。

ではfastRemoveメソッドを見ていきます。
private void fastRemove(int index) { modCount++; int numMoved = size - index - 1; if (numMoved > 0) System.arraycopy(elementData, index+1, elementData, index, numMoved); elementData[--size] = null; // clear to let GC do its work }
modCountはインクリメントされて、numMovedには4-2-1で1が入ります。
numMovedが0より大きいので、System.arraycopyが実行され、array[3]に入っていたDがarray[2]にコピーされます。
そしてarray[3]にnullを入れて戻ります。
このときiの位置はまだ動いていません。

このあと拡張for文の処理でhasNextメソッドを実行します。
すると
cursor != size()
がtrueになるのでnextメソッドを実行せずに終了します(cursor=i+1=3、size()の戻り値も3)。
逆に削除する要素が最後から2番目の要素でない場合、対象の要素を削除した後でこれがfalseになるのでnextメソッドが呼ばれcheckForComodificationが実行されます。
例えば一番最後の要素を削除した場合はこのようになります(cursor=i+1=4、size()の戻り値は3)。

modCountはfastRemoveメソッドの中でインクリメントされてexpectedModCountとは異なる値になっているので、ConcurrentModificationExceptionがスローされます。
【基本・応用情報技術者】真理値表の使い方
こんにちは。たろすです。
今回は真理値表の使い方を説明します。
基礎
真理値表は論理式の変形が難しい場合などに役立ちます。
まず基礎的な説明からしていきます。
積
扱う変数が2つの場合、それぞれの変数がとり得る値の組み合わせは
の4通りです。
と
の列にはこの組み合わせを書きます。
そしての列を埋めていきます。
が1となるのは
と
がともに1のときなので、
のときは0、
のときは1 が入ります。
(なぜが1となるのは
と
がともに1のときなのかというと、そういう決まりだからです。)

和
同様にと
の列を作り、
の列を埋めていきます。
が1となるのは
か
のどちらかあるいは両方が1のときなので、
のときは0、
のときはは1が入ります。

含意
同様にと
の列を作り、
の列を埋めていきます。
が0となるのは
が1で
が0のときなので、
のときは0、
のときは1が入ります。

否定
の列を作り、
の列を埋めていきます。
これは値を反転させるだけです。

Java Silver合格への道 ~受験編~
こんにちは。たろすです。
Java Silverを受験してきたので、過程と結果を報告します。
勉強期間と方法
4か月の間、週に2日、1日2~3時間程度勉強しました。
この期間に黒本を3周しました。
最後の方にはほとんど間違えなくなっていたので、経験者なら3周すれば十分かと思います。
ちなみに黒本というのはこれのことです。
私は安かったので初版を買いましたが、最新のものを買うことをおすすめします。
誤植が結構多かったので。。。
とはいえ、得点に直結するようなクリティカルな誤植はそれほどなかったので、安さ重視なら初版でもOKです。
他の参考書は必要?
Java Silverの参考書として紫本や白本と呼ばれるものがありますが、経験者なら必要ないです。
逆に言うと、Java自体がほぼ初めてという方は買っておいてもよいかと思います。
紫本と白本は以下の本を指してます。
結果
結果はその場で見ることができます。
正解率はなんと94%でした。
合格ラインが65%なので余裕の合格です。
黒本で見た問題もいくつかあったので、やはり黒本を完璧にしておいたのは正解でした。






